hastel.blogg.se

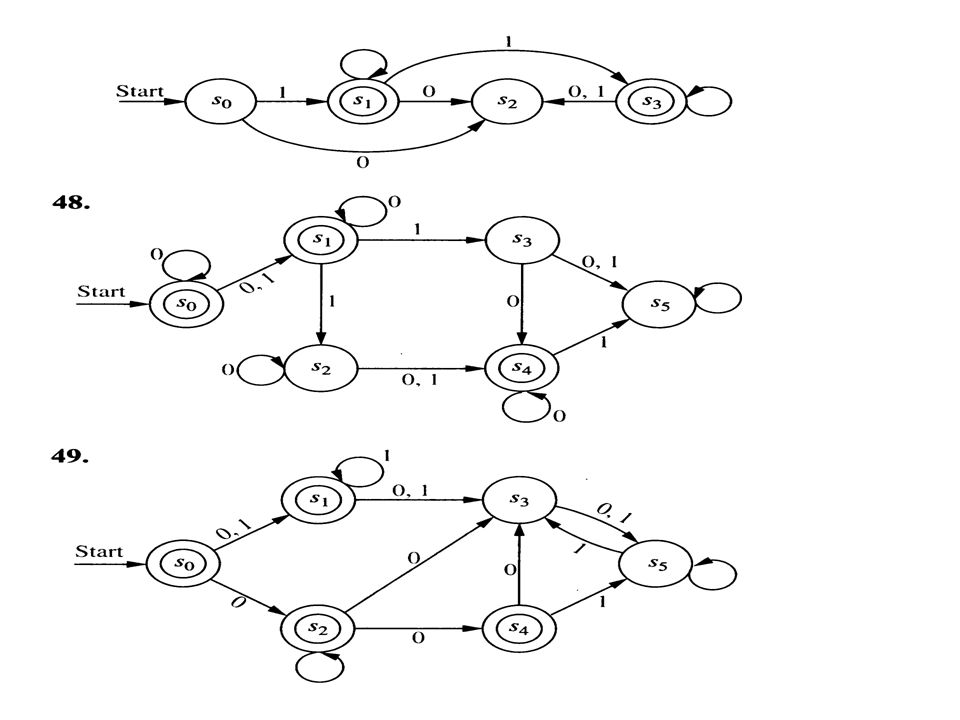
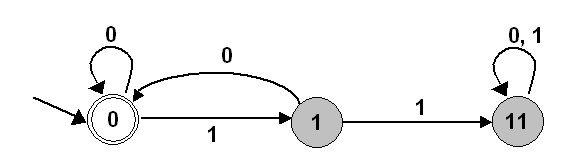
$$L(A) = (a \cup b^2 \cup b a^2 \cup b a b)^* ba $$ as one can validate easily. Obviously, the theory computation and the theory of formal language are just. Thus the language accepted by the automaton is That is a string is accepted by a DFA if and only.

Language accepted by DFA Contents Here we are going to formally define what is meant by a DFA (deterministic finite automaton) accepting a string or a language. \Xi_0 = (a \cup b^2 \cup b a^2 \cup b a b)^* ba Language Accepted by DFA Subjects to be Learned. \Xi_0 = a \cup (b^2 \cup b a^2 \cup b a b) \Xi_0 \cup ba It’s also called the language decided/accepted by M. A string is accepted (or recognized) if the FSA ends in one of its final. \Xi_0 = a \Xi_0 \cup b ((b \cup a ((a \cup b)) \Xi_0 \cup a) start state (q 0) accept states (F) transitions Anatomy of a Deterministic Finite The alphabet of a finite automaton is the set where the symbols come from, for The language L(M) of a finite automaton is the set of strings that it accepts The singular of automata is automaton. When they have no output, FSMs are often called finite state automata (FSA). Substituting to the first equation we get Languages recognized by finite automata Proposition 4 expresses the fact that languages consisting of a single word consisting itself of a single letter are. The process of finding the language accepted by an automaton $A = (Q,\Sigma, \delta, q_0, F)$ involves solving a system of equations over the monoid $(\Sigma, \circ, \epsilon)$ with $\epsilon$ denoting the empty word of the alphabet.ĭenote as $\Xi_i$ the language recognized by the automaton $(Q, \Sigma, \delta, q_i, F)$ and $Q= \left\) Indeed, there is an elegant way to compute this.